Question

You are designing a rectangular garden. the garden will be enclosed by fencing on three sides and by a house on the fourth side. you want the garden to have an area of 288 square feet, but you want to minimize the amount of fencing that you need. how many feet of fencing do you need to enclose the garden?

Answer 1

Suppose the dimensions of the rectangle is x by y and let the side enclosed by a house be one of the sides measuring x, then the sides that is to be enclosed are two sides measuring y and one side measuring x.

Thus, the length of fencing needed is given by

P = x + 2y

The area of the rectangle is given by xy,

i.e.


`xy = 288 \\ \\ \\ \\ \Rightarrow y= (288)/(x)`

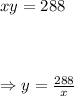
Substituting for y into the equation for the length of fencing needed, we have


`P=x+2\left( (288)/(x) \right)=x+ (576)/(x)`

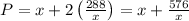
For the amount of fencing to be minimum, then


`(dP)/(dx) =0 \\ \\ \Rightarrow1- (576)/(x^2) =0 \\ \\ \Rightarrow (576)/(x^2) =1 \\ \\ \Rightarrow x^2=576 \\ \\ \Rightarrow x=√(576)=24`

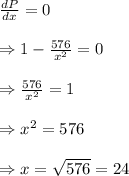
Now, recall that


`y= (288)/(x) = (288)/(24) =12`

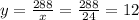
Thus, the length of fencing needed is given by

P = x + 2y = 24 + 2(12) = 24 + 24 = 48.

Therefore, 48 feets of fencing is needed to enclose the garden.