Final answer:
Upon calculating, the volume of the square pyramid box is 51.84 inches³ and the total volume for 20 pieces of candy is 16 inches³. Since the box volume is greater than the candy volume, Rebecca can fit 20 pieces of candy into each box.
Step-by-step explanation:
The student's question is about determining whether 20 pieces of candy can fit into a square pyramid-shaped box, given the dimensions of the box and the volume of each candy piece. To solve this, we need to calculate the volume of the square pyramid box and compare it to the total volume of the candy pieces.
The volume (V) of a square pyramid can be found using the formula:
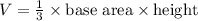
For a pyramid with a square base:
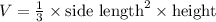
Plugging in the given dimensions:
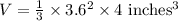
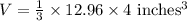
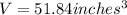
Next, we find the total volume occupied by 20 pieces of candy:
Total candy volume =
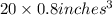
Total candy volume =
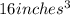
Since the volume of the pyramid (51.84
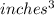 ) is greater than the total volume of the candies (16
) is greater than the total volume of the candies (16
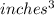 ), Rebecca will be able to fit 20 pieces of candy into each candy box.
), Rebecca will be able to fit 20 pieces of candy into each candy box.