The system is:
i) y=-2x+3
ii)
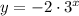
.
Making y's equal, we have:
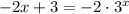
.
Dividing all terms by -2, we have:
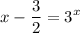
.
Note that
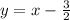
is an increasing linear function. (Its graph is the same as y=x, only shifted 3/2 units down.)
The graph of this function is below the x-axis up to 3/2, where it cuts the x-axis, and then increases above the x-axis making an angle of 45° with the x-axis.
The graph of
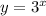
is completely above the x-axis, and it rises much faster than the line. We could compare at 3/2, for example, where the linear function is 0. The exponential function takes the value
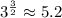
and is increasing very fast.
Thus, the graphs never meet, which means the system has no solution.
Answer: no solution.