Answer: The correct option is
(D) x = 29, y = 49, z = 102.
Step-by-step explanation: We are given to find the values of the variables x, y and z in the parallelogram shown.
Let us label the given parallelogram as ABCD, shown in the attached figure.
Here,
m∠CAB = 29°, m∠ABC = 102°.
Now, since AB is parallel to CD and AC is a transversal. So,
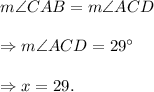
Now, in triangle ABC, we have
![m\angle ABC+m\angle ACB+m\angle BAC=180^\circ~~~~~~~~\textup{[angle sum property of a triangle]}\\\\\Rightarrow 102^\circ+y^\circ+29^\circ=180^\circ\\\\\Rightarrow y^\circ+131^\circ=180^\circ\\\\\Rightarrow y^\circ=180^\circ-131^\circ\\\\\Rightarrow y^\circ=49^\circ\\\\\Rightarrow y=49.](https://img.qammunity.org/2018/formulas/mathematics/high-school/ann4h33o3i9sc1w5v4iiz12isa18s2d0hp.png)
Again, we know that the measures of the opposite angles of a parallelogram are equal.
So,
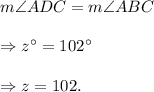
Thus, the required values are
x = 29, y = 49, z = 102.
Option (D) is CORRECT.