Question

The lines whose equations are 2x + y = 3z and x + y = 6z intersect at which point? (3z, -3z) (-3z, 9z) (9z, -15z)

Answer 1

equation 1 - equation 2: (2x-x)=3z-6z, so x=-3z.
2(-3z)+y=3z, so y=9z
(-3z, 9z) is the answer.

Answer 2

The lines whose equations are 2x + y = 3z and x + y = 6z intersect at the point (-3z,9z)

Explanation:

When two straight lines intersect, they coincide only at one point. This point is described through a set of "x" and "y" coordinates, usually expressed as a point (x, y). Because both lines pass through that point, you know that the coordinates (x, y) must satisfy both equations. Therefore it is possible to establish a system of two equations with two unknowns or variables :

`\left \{ {{2*x+y=3*z} \atop {x+y=6*z}} \right.`

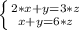
This system of equations can be solved by several methods. In this case it is decided to solve it by the substitution method. This method consists of isolating one of the variables and replacing its expression in the other equation. In this case, the value of "y" is isolated from the second equation of the system of equations, obtaining:

y=6*z-x

Substituting in the first equation of the system of equations, the following first degree equation is obtained:

2*x+6*z-x=3*z

This equation is solved:

2*x-x=3*z-6*z

x=-3*z =-3z

In this way the value of "x" is obtained, whose value is -3*z (or -3z). To obtain the value of "y", the value of "x" obtained in the equation where the value of "y" was previously isolated is substituted:

y=6*z-x

y=6*z-(-3*z)

y=6*z+3*z

y=9*z=9z

In this way the value of "y" is obtained, whose value is 9*z (or 9z).

The lines whose equations are 2x + y = 3z and x + y = 6z intersect at the point (-3z,9z)