Question

Write the inverse of 5x – 17 = 11 + 3y in f–1(x) notation.
*Show your work*

Answer 1

In the first step i swapped the places of x and y

Answer 2

`f^(-1)(x)=(3)/(5)x+(28)/(5)`

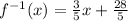
Step-by-step explanation:

The given equation is

`5x - 17 = 11 + 3y`

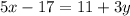
We need to find the inverse of the function.

Step 1: Interchange x and y.

`5y - 17 = 11 + 3x`

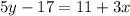
Step 2: Isolate y on left side.

Add 17 on both sides.

`5y - 17+17= 11 + 3x+17`

`5y=3x+28`

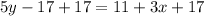
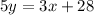
Divide both sides by 5.

`y=(3x+28)/(5)`

`y=(3)/(5)x+(28)/(5)`

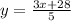
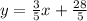
Step 3: Substitute
`y=f^(-1)(x)`.

`f^(-1)(x)=(3)/(5)x+(28)/(5)`

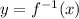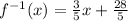
Therefore, the inverse of the function is
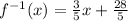`f^(-1)(x)=(3)/(5)x+(28)/(5)`.