Answer:
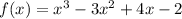
Explanation:
we know that
The conjugate root theorem states that if the complex number a + bi is a root of a polynomial P(x) in one variable with real coefficients, then the complex conjugate a - bi is also a root of that polynomial
In this problem we have that
The polynomial has roots 1 and (1+i)
so
by the conjugate root theorem
(1-i) is also a root of the polynomial
therefore
The lowest degree of the polynomial is 3
so
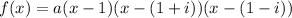
Remember that
The leading coefficient is 1
so
a=1
![f(x)=(x-1)(x-(1+i))(x-(1-i))\\\\f(x)=(x-1)[x^(2) -(1-i)x-(1+i)x+(1-i^2)]\\\\f(x)=(x-1)[x^(2) -x+xi-x-xi+2]\\\\f(x)=(x-1)[x^(2) -2x+2]\\\\f(x)=x^(3)-2x^(2) +2x-x^(2) +2x-2\\\\f(x)=x^(3)-3x^(2) +4x-2](https://img.qammunity.org/2018/formulas/mathematics/high-school/i2gvps6lc28ln4xzjdfdqqc8t0znm2vlfk.png)