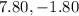Question

Solve for x in the equation 3x^2-18x+5=47

Answer 1

`x = 3+- √(23)`

Answer 2

`x`≅
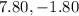`7.80,-1.80` (rounded to 2 decimal places)

Explanation:

This is a quadratic equation :
`3x^2-18x+5=47`

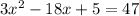
Bringing everything to left side:

`3x^2-18x+5=47\\3x^2-18x+5-47=0\\3x^2-18x-42=0`

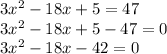
We can use the quadratic formula to find the value(s) of x:

Quadratic Formula:

• 
  `x=(-b+√(b^2-4ac) )/(2a)`

and

• 
  `x=(-b-√(b^2-4ac) )/(2a)`

Where,

• a is the coefficient of
  `x^2`
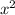
• b is the coefficient of
  `x`
• c is the constant term

For our question we have:

`a=3\\b=-18\\c=-42`

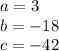
Plugging in all the values we get:

`x=(-(-18)+√((-18)^2-4(3)(-42)) )/(2(3))\\x=(18+√(828) )/(6)`

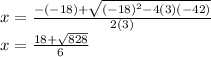
This is approximately 7.80

and

`x=(-(-18)-√((-18)^2-4(3)(-42)) )/(2(3))\\x=(18-√(828) )/(6)`

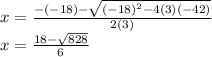
This is approximately -1.80

So,
`x`≅
`7.80,-1.80`