Question

For what values of x is log base 0.8 (x+4)>log base 0.4 (x+4)
Thank you!

Answer 1

We are seeking the solution of the inequality:


`\displaystyle{ \log_(0.8)(x+4)\ \textgreater \ \log_(0.4)(x+4)`.


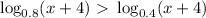
We recall that a log function
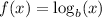
`f(x)=\log_b(x)` is either increasing or decreasing:

i) it is increasing if b>1,

ii) it is decreasing if 0<b<1.

Consider the functions
`\displaystyle{ \log_(0.8)(x)` and
`\displaystyle{ \log_(0.4)(x)`.

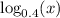
The graphs of these functions both meet at x=1 (clearly), and after 1 they are both negative. So from 0 to 1 one of them is larger for all x, and from 1 to infinity the other is larger. (Being strictly decreasing, their graphs can only intersect once.)


We can check for a certain convenient point, for example x=0.8:


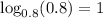
`\displaystyle{ \log_(0.8)(0.8)=1` and


`\displaystyle{ \log_(0.4)(0.8)=\log_(0.4)(0.4\cdot 2)=\log_(0.4)(0.4)+\log_(0.4)(\cdot 2)=1+\log_(0.4)(2)`.

Now,
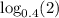
`\displaystyle{ \log_(0.4)(2)` is negative since we already explained that for x>1 both functions were negative. This means that


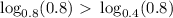
`\displaystyle{ \log_(0.8)(0.8)\ \textgreater \ \log_(0.4)(0.8)`, and since
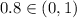
`0.8\in (0, 1)`, then this is the interval where
`\displaystyle{ \log_(0.8)(x)\ \textgreater \ \log_(0.4)(x)`.


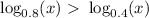
So, now considering the functions
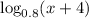
`\displaystyle{ \log_(0.8)(x+4)` and
`\displaystyle{ \log_(0.4)(x+4)`, we see that

x+4 must be in the interval (0,1), so we solve:

0<x+4<1, which yields -4<x<-3 after we subtract by 4.


Answer: (-4, -3). Attached is the graph generated using Desmos.