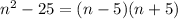Answer:
The factor form of:
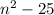 is:
is:
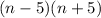
Explanation:
Factor form--
It means that the expression is represented by factoring the expression.
i.e. we find out the roots of the expression and then express it as a product of it's linear factors.
The expression is given by:
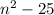
We know that any expression of the form:
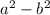 could be written in the form:
could be written in the form:
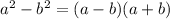
Here we have:
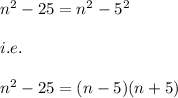
Hence, the answer is: