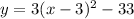The standard form of a quadratic equation is
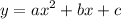
, while the vertex form is:

, where (h, k) is the vertex of the parabola.
What we want is to write

as

First, we note that all the three terms have a factor of 3, so we factorize it and write:
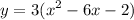
.
Second, we notice that

are the terms produced by
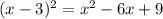
, without the 9. So we can write:
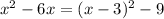
, and substituting in
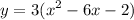
we have:
![\displaystyle{ y=3(x^2-6x-2)=3[(x-3)^2-9-2]=3[(x-3)^2-11]](https://img.qammunity.org/2018/formulas/mathematics/high-school/i8o99s7hqjhrpnvrkxa4tplwbkui0cbjx2.png)
.
Finally, distributing 3 over the two terms in the brackets we have:
![y=3[x-3]^2-33](https://img.qammunity.org/2018/formulas/mathematics/high-school/jicgrtshbv0gcbvf03k04a0z3o5g8oupgm.png)
.
Answer: