Answer: "
2.989 cm² " .
__________________________Step-by-step explanation:__________________________Let "A" represent the "area" ;
"L" represent the "Length" ;
"w" represent the "width" ;
"P" represent the "Perimeter".
_________________________Note the following equations /formulas for a rectangle:
A = L * w ;
P = 2L + 2w ;
Given: "L = 2w " ;
and: " P = 7

cm" ; Solve for "A" ;
___________________________________________ 7

cm = 2L + 2w ;
Divide EACH side by "2" ;
_____________________________ 7

cm / 2 = (2L + 2w) / 2 ;
to get:
7

cm / 2 = L + w ;
Given: L = 2w ; rewrite the above equation; substituting "2w" for "L" ;
______________________________________________________
7

cm / 2 = 2w + w ;
7

cm / 2 = 3w ;
______________________________
Note:
______________________________ 7

cm / 2 ;
=
![([(3*7) + 1])/(3)](https://img.qammunity.org/2018/formulas/mathematics/middle-school/qv9kqb5rb4r7jhyyt3accqyagpr5go5xfm.png)
cm / 2 ;
=
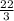
cm / 2 ;
=

*
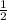
;
Note: The "22 cm" cancels to "11 cm" ; and the "2" cancels out to "1" ;
{Since: "(22 cm ÷ 2 = 11 cm)" ; and since: "(2 ÷ 2 = 1)" .
And we can rewrite the expression as:
____________________________________________ 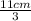
*
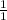
;
and further simplify:
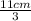
*
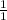
;
=
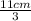
* 1 ;
=
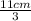
;
____________________________________________
Now, we can take the equation:
7

cm / 2 = 3w ;
____________________________________________and rewrite as:
____________________________________________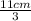
= 3w ;
and multiply each side by "

" ; to isolate "w" on one side of the equation ; and to solve for "w" ;
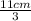
*

= {3w} *

;
to get:

= w ;
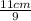
= w ;
↔ w =

cm ;
___________________________________
Given: L = 2w ;
L = 2 *

cm ;
L = {
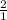
*

} cm ;
L =
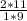
cm ;
L =
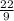
cm ;
____________________________________Now, solve for "A" (area):
A = L * w ;
A =
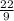
cm *

cm ;
A =
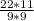
cm² ;
A =

cm² ;
A = 2.9876543209876543 cm² ; round to: "
2.989 cm² " .
____________________________________________________