We first need to factorize (if possible) the denominators:
we can see that
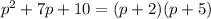
as 2 and 5 are two numbers whose sum is 7 and product is 10.
Similarly, we can see that
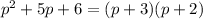
as 2 and 3 are two numbers whose sum is 5 and product is 6.
Thus, the expression is:
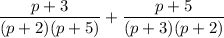
.
Now to make the denominators equal, but to also keep them as small as possible, the common denominator must be (p+3)(p+2)(p+5).
Answer: (p+3)(p+2)(p+5).