Question

Let f(x) = -20x^2 + 14x + 12 and g(x) = 5x- 6. Find f/g and state its domain

Answer 1

f(x) = -20x²+14x+12 and g(x) = 5x-6


`(f(x))/(g(x)) = (-20 x^(2) + 14x+12)/(5x-6)`

`= (-(20 x^(2) -14x-12))/(5x-6)`

`(-[20 x^(2)-24x+10x-12] )/(5x-6)`
=
`(-[2x(10x-12)+1(10x-12)])/(5x-6)`
=
`(-[(2x+1)(10x-12)])/(5x-6)`
=
`(-2(2x+1)(5x-6))/(5x-6)`
=
`-2(2x+1)`

Now, since this is a linear equation, it is defined at every real number.
Therefore, domain is x∈(⁻∞,⁺∞)

Answer 2

-2(2x+1)

Domain : (-∞, 5/6) U (5/6 , ∞)

Explanation:

f(x) = -20x^2 + 14x + 12 and g(x) = 5x- 6

`f/g= (f(x))/(g(x)) = (-20x^(2) + 14x+12)/(5x-6)`

Factor -20x^2 +14x+12, GCF is -2

-2(10x^2-7x-6)

we find two factors whose product is -60 and sum is -7

-12* 5= -60

-12+5 = -7

-2(10x^2-12x+5x-6)

-2((10x^2-12x)+(5x-6)

-2(2x(5x-6)+1(5x-6))

-2(2x+1)(5x-6)

Replace it in the numerator

`(-2(2x+1)(5x-6))/(5x-6)`

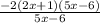
Cancel out 5x-6

So it becomes -2(2x+1)

To get the domain , we ignore the values of x that makes the denominator 0 in the original f(x)/ g(x)

we set denominator =0 and solve for x

5x-6=0

5x=6

divide by 5

x= 5/6

domain is all real numbers except 5/6

(-∞, 5/6) U (5/6 , ∞)