Answer: A,B and C are true.
Explanation:
let f(x) be the given polynomial with variable x such that
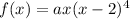 m,where a be any odd degree negative leading coefficient of f(x),x has root as 0 with multiplicity 1 and
m,where a be any odd degree negative leading coefficient of f(x),x has root as 0 with multiplicity 1 and
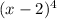 has root 2 with multiplicity 4.
has root 2 with multiplicity 4.
Lets check all the options
A. The function is positive on (-∞, 0)
let x=-1∈(-∞, 0)
⇒
 > 0 as a is negative.
> 0 as a is negative.
∴ function is positive on (-∞, 0) .i,e. A is true.
B. The function is negative on (0, 2).
Let x=1 ∈(0,2)
⇒
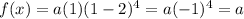 < 0 as a is negative.
< 0 as a is negative.
∴ the function is negative on (0, 2) .i,e. B is true.
C. The function is negative on (2, ∞)
let x=3∈(2,∞)
⇒
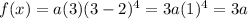 < 0 as a is negative.
< 0 as a is negative.
∴ the function is negative on (2,∞).
D.The function is positive on (0, ∞) which is not true from C.