Question

A data set of values has a mean of 45 and standard deviation of 5. The z-score for a point A is 0. The z-score for a point B is0.2. What are the values of point A and point B?

Answer 1

Point B Is 36.

hope this helped

Answer 2

Given;

A data set of values has a mean of 45 and standard deviation of 5.

The z-score for a point A is 0. The z-score for a point B is 0.2.

To find the values of A and B, we will apply the z-score formula, which is

`\begin{gathered} z=(x-\mu)/(\sigma) \\ Where\text{ } \\ x\text{ is the observed value} \\ \mu\text{ is the mean} \\ \sigma\text{ is the standard deviation} \end{gathered}`

Where

`\begin{gathered} \mu=45 \\ \sigma=5 \end{gathered}`

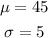
For the value of point A,

Where, z = 0 for point A

`\begin{gathered} z=(x-\mu)/(\sigma) \\ 0=(x-45)/(5) \\ Crossmultiply \\ 5(0)=x-45 \\ 0=x-45 \\ x=45 \end{gathered}`

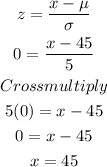
Hence, the value of point A is 45

For the value of point B,

Where, z = 0.2 for point B

`\begin{gathered} z=(x-\mu)/(\sigma) \\ 0.2=(x-45)/(5) \\ Crossmultiply \\ 0.2(5)=x-45 \\ 1=x-45 \\ Collect\text{ like terms} \\ x=1+45=46 \\ x=46 \end{gathered}`

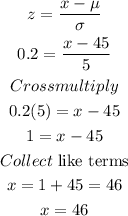
Hence, the value of point B is 46