Answer:
1.
 1 2.
1 2.
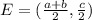 4 3.
4 3.
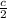 8 4. AC, BD 5. CE, DE 6.
8 4. AC, BD 5. CE, DE 6.
Explanation:
Below each answer the respective explanation, and also a numerical coordinate parallelogram just to make it clearer.
According to the graph
A= (0,0)
B= (a,0)
C= (a+b, c)
D=(b,c)
E=(a+b/2, c/2)
1. The coordinates of point C are

To find the x-coordinate of C: just add a to b

2. The coordinates of the midpoint of diagonal AC are (__, c/2 ).
Midpoints are calculated by:
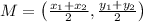
Since A (0,0) and C (a+b,c) Then: (a+b/2, c/2)
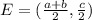
3. The coordinates of the midpoint of diagonal BD are (a+b/2, __).
Then
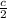 (8)
(8)
4. ___ and ___ intersect at point E with coordinates (a+b/2, c/2)
AC and BD . True. This is a consequence of steps 2 and 3.
5. By the definition of midpoint, AE≅ __ and BE≅ __.
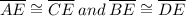
6.Therefore, diagonals AC and BD bisect each other.
In this sense, to bisect is to equally divide into two congruent line segments.