ANSWER
The length of the shadow is

Step-by-step explanation
The shadow cast by the building is
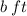
long.
We use trigonometry to determine the length of b.

is the length of the side that is adjacent to the 20° angle.
We also know the length of the side that is opposite to the 20° angle to be 150ft.
We now use the tangent ratio to determine the value of b.
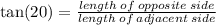
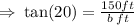
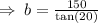
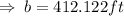
To the neatest feet,the length of the shadow is
