Question

Find the polynomial function with the following roots: -1 of multiplicity 2; and 3.

Answer 1

to the risk of being redundant.

multiplicity of a root means, is there many times, so a multiplicitiy of 2 on -1 means is there twice, so,


`\bf \begin{cases} x=-1\implies &x+1=0\\ x=-1\implies &x+1=0\\ x=3\implies &x-3=0 \end{cases} \\\\\\ (x+1)(x+1)(x-3)=\stackrel{\textit{original polynomial}}{y} \\\\\\ (x+1)^2(x-3)=y\implies (x^2+2x+1)(x-3)=y \\\\\\ x^3+2x^2+x-3x^2-6x-3=y\implies x^3-x^2-5x-3=y`

Answer 2

Think of "multiplicity" as "exponents of the roots". So now "roots" have to do with x values. We need roots where x = 0, -1 means that "x+1=0", because when x=-1, -1+1=0, that statement is true. Since that "x+1" has a multiplicity of 2, we'll square that value:

`{(x + 1)}^(2)`
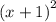
The single root of 3 can be written as "x-3=0", because plugging in 3 for x makes that statement true: 3-3=0
Now we combine the terms by multiplying them and set that equal to 0:

`{(x + 1)}^(2) (x - 3) = 0`