Answer:
C)
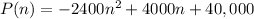
Explanation:
Since, profit = number of car sold × total markup
Original markup = $2,000
Also, the original number of sold cars = 20,
Let the markup is decreases by n times of $400,
New markup = ( 2000 - 400n ) dollars,
According to the question,
For each $400 decrease in markup an additional 6 cars are sold.
So, new number of sold cars = 20 + 6x,
Hence, the total monthly profit P(n) would be,
P(n) = ( 2000 - 400n )( 20 + 6n )
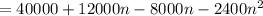
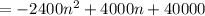
Option 'C' is correct.