Question

A car dealership sells 20 cars when there is a $2,000 markup over the factory price of each vehicle. The sales department determines that for each $400 decrease in markup an additional 6 cars are sold. Write a function that models the total monthly profit P(n). Let n represent the number of markdowns.

A) P(n) = 2400n2 + 4000n + 40,000
B) P(n) = 2400n2 − 4000n + 40,000
C) P(n) = −2400n2 + 4000n + 40,000
D) P(n) = −2400n2 − 4000n + 40,000

Answer 1

C
P(n) = total monthly profit
Let n = number of markdowns
Total profit = (Markup per car)(Number of car sales)
P(n) = (2000 − 400n)(20 + 6n)
P(n) = −2400n2 + 4000n + 40,000

Answer 2

C)
`P(n) = -2400n^2 + 4000n + 40,000`

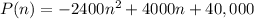
Explanation:

Since, profit = number of car sold × total markup

Original markup = $2,000

Also, the original number of sold cars = 20,

Let the markup is decreases by n times of $400,

New markup = ( 2000 - 400n ) dollars,

According to the question,

For each $400 decrease in markup an additional 6 cars are sold.

So, new number of sold cars = 20 + 6x,

Hence, the total monthly profit P(n) would be,

P(n) = ( 2000 - 400n )( 20 + 6n )

`= 40000 +12000n - 8000n- 2400n^2`

`=-2400n^2+4000n+40000`

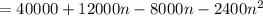
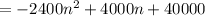
Option 'C' is correct.