Answer:
Zero with the subscripts, +2 without them.
Step-by-step explanation:
Hello!
In this case, since we consider that two silicon are bonded with four oxygen atoms to form silicon oxide according to the following chemical equation:
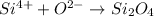
It is also possible to realize it can be simplified to obtain:
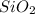
Which means that the total charge with the subscripts is zero, and without the subscripts +2 (+4-2).
Best regards!