Question

Write an equation in standard form for the circle shown.

A) (x + 3)2 + (y – 1)2 = 7
B) (x - 3)2 + (y + 1)2 = 7
C) (x + 3)2 + (y – 1)2 = 49
D) (x - 3)2 + (y + 1)2 = 49

Answer 1

radius = 7
center = (-3, 1)

Equation for a circle is: r² = (x-h)² + (y-k)²
where r = radius, (h,k) = center
fill in the values to get:
7² = (x+3)² + (y-1)²

Answer is C

Answer 2

Answer: C)
`(x+3)^2+(y-1)^2=49`

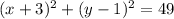
Explanation:

From the given figure it can be seen that the centre of the circle is at (-3,1)

and the distance from the center to the boundary = 7 units.

i.e. radius of the given circle = 7 units

We know that , the standard equation of circle is given by :-

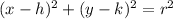`(x-h)^2+(y-k)^2=r^2`, where (h,k) represents the center of the circle and r represents the radius of the circle.

Therefore, the equation of the given circle will be:-

`(x-(-3))^2+(y-1)^2=7^2\\\\\Rightarrow\ (x+3)^2+(y-1)^2=49`