Answer:
The correct option is C.
Explanation:
A geometric series divergent if
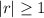 .
.
In the first option the first term of the series is,
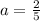
common ratio is
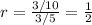
Since the common ratio is less than 1, therefore the geometric series is convergent and the option A is incorrect.
In the second option the first term of the series is,

common ratio is
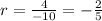
Since the common ratio is less than 1, therefore the geometric series is convergent and the option B is incorrect.
The nth term of a geometric series is in the form of
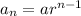
So, the common ratio of option C and D are -4 and
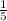 respectively.
respectively.
Since the absolute common ratio in option C is more than 1. i.e.,
 , therefore the geometric series is divergent and the option C is correct.
, therefore the geometric series is divergent and the option C is correct.
Since the common ratio in option D is less than 1, therefore the geometric series is convergent and the option D is incorrect.