Answer:
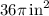
Explanation:
The surface area of a cylinder is defined as the surface area of the side + the surface area of its bases, which are circles.
First, find the surface area of the bases using the formula:
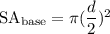


Next, find the surface area of the sides, which is the circumference of the bases multiplied by the height of the cylinder:
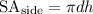
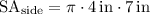
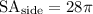
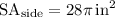
Finally, to find the surface area of the entire cylinder, add the area of the bases and the area of the side together (remember there are 2 bases):
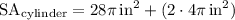

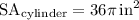
So, the candle has a surface area of
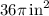 .
.