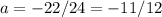Question

Suppose h(x) = ax^3 + 11x^2. Determine a if h has an inflection point at x = 4. Show all your work.

Answer 1

This isn't the answer, but do you have the rest of the questions?

Explanation:

Thank you in advance.

Answer 2

`a=-11/12`

Explanation:

We are given the function:

`h(x)=ax^3 + 11 x^ 2`

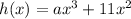
And we want to determine a such that h(x) has an inflection point at x = 4.

Possible inflection points are whenever h''(x) equals 0. So, we will first differentiate h(x) twice. This yields:

`h'(x)=3ax^2+22x`

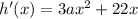
So:

`h^(\prime\prime) (x)=6ax+22`

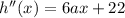
Inflection points occur when h''(x) = 0. So:

`0=6ax+22`

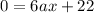
Since we have an inflection at x = 4:

`0=24a+22`

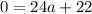
And solving for a yields:

`a=-22/24=-11/12`