Parallel toy= (3)/(4) x-4; through (-4,1)

Question

Parallel to
`y= (3)/(4) x-4`; through (-4,1)

Answer 1

Answer: " y =
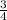`(3)/(4)` x + 4 " .
_________________________________________________
Step-by-step explanation:
_________________________________________________
We are given an equation in "slope intercept form" ; that is; in the form of :

"y = mx + b" ; in which "y" in isolated on the left-hand side of the equation; with "no-coefficient" (except for the "implied coefficient" of "1");

in which: "m" is the slope of the line; and the coefficient of "x"; and "b" is the "y-intercept" (or the value of the "y-coordinate" of the graph when "x = 0" ;
______________________________________________
We are given: " y =
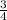
`(3)/(4)`x − 4 " ;

in which the slope; "m", is "
`(3)/(4)`" .

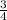
Since we want to write the equation, in slope-intercept form, for the line PARALLEL to the given line; we known that the "line" that is "parallel" will have the same slope".

So we can write: " y =
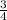
`(3)/(4)` x + b" .

Note that we are instructed to find the "parallel line" that passed through:

"(-4, 1)" ;
______________________________________________________
So, in the aformentioned equation, we substitute "-4" for "x" ; and "1" for "y"; to solve for "b" ;
______________________________________
y =
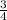
`(3)/(4)` x + b ;

1 =
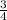
`(3)/(4)` * -4 + b ;

→ 1 = -3 + b ;

↔ b + (-3) = 1 ;

↔ b − 3 = 1 ;

Add "3" to each side of the equation:

b − 3 + 3 = 1 + 3 ;

→ b = 4 .
______________________________
Now, since we now that "b" is "positive 4" ; we can write the equation of the parallel line:

" y =
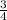`(3)/(4)` x + 4 " .
__________________________________________________