Question

Find the unknown side of the right triangle below. Round to the nearest tenth .

Answer 1

`2.2 km`

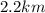
Skills needed: Pythagorean Theorem

Explanation:

1) We are given a right triangle. A right triangle has one right angle, which has a measure of 90 degrees.

- This theorem is used to find the side lengths of a right triangle. This problem is a perfect example for using this theorem.

------------------------------------------------------------------------------------------------------------- 2) Before using this theorem, there are some important vocab terms:

---> Legs: Legs are the two shorter sides of a right triangle. They are not opposite the right angle.

---> Hypotenuse: This is the side that is opposite of the right angle, and is also the longest side of the right triangle.

In the theorem below,
`a` and
`b` are the legs,
`c` is the hypotenuse

-------------------------------------------------------------------------------------------------------- 3) The theorem (essentially a formula) is:

`a^2+b^2=c^2`

Now, let's determine which side is which variable:

- We are given
`a`, which is 2, which is a leg.

- We are also given
`c`, which is 3, which is the hypotenuse (since it is opposite of the right angle)

Let's plug it in below:

`2^2+b^2=c^2`, so we are solving for
`b`, the other leg.

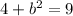`4+b^2=9` (simplifying the exponents)

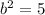`b^2=5` (isolating the
`b` to solve)

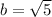`b=√(5)` (square-rooting both sides to solve for "b")

`b = \sqrt5=2.2`

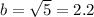
square root 5 is rounded to 2.2, so that is the answer.