Via subsitution we want to isolate x for 6x - 4y = 36
Start by adding 4y to both sides.
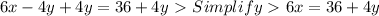
Now divide both sides by 6
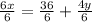
.
Now simplify further.
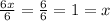
Apply the rule of
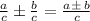
to
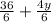
When applied >
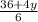
> Now factor 36 + 4y > Rewrite it as....
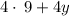
> Factor out the common term of 4 >
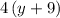
This gives us
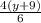
From there we want to cancel the common factor of 2 which gives us...
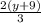
Now you want to
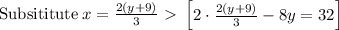
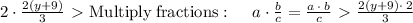
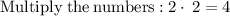
This gives us
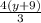
So now we have
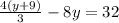
We want to multiply both sides by 3.
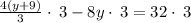
Refine it.

Expand
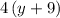
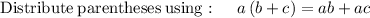
Where
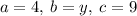
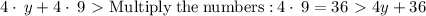
So now we have
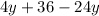
Group the like terms.
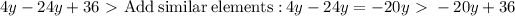
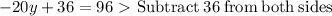
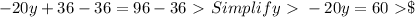
Now we want to
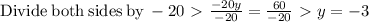
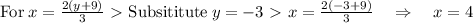
Therefore our final solutions are, y = -3, x =4.
Hope this helps!