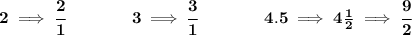Question

The graph of f(x) = 2x^3 -19x^2 + 57x-54 is shown below. How many roots of f(x) are rational numbers? The options are 0,1,2,3

Please please help

Answer 1

Answer: its 3

Explanation:

Answer 2

recall from the "fundamental theorem of algebra", that the polynomial will have as many roots as its degree.

notice, this is a cubic polynomial, thus it has a 3rd degree, thus 3 roots as well.

now, a rational number is one you can write and represent as a "ration", or fraction.

by looking at the graph, check the picture below, the solutions, namely where the graph touches the x-axis, are


`\bf 2\implies \cfrac{2}{1}\qquad \qquad 3\implies \cfrac{3}{1}\qquad \qquad 4.5\implies 4(1)/(2)\implies \cfrac{9}{2}`