Question

State the horizontal asymptote of the rational function. f(x) = x+9÷x^2+2x+3

Answer 1

Assuming you know the asymptote rules. We want to use the one that states if numerator's degree = 1 + denominators degree, the asymptote is a slant symptote in the form of y = mx + b.

`\lim_(n \to \infty) (f(x))/(x) \ \textgreater \ \lim_(n \to \infty) [tex] \lim_(n \to \infty) ( (x + 9)/(x^2) + 2x + 3 - 2x) \ \textgreater \ refine \ \textgreater \ \lim_(n \to \infty) ( (x + 9)/(x^2) + 3)` \ \textgreater \ 2 [/tex]
Now write the exception of indeterminate form.

`\lim_(n \to \infty) ( (x + 9)/(x^2) \lim_(n \to \infty)3`
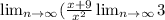
For
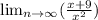
`\lim_(n \to \infty) ( (x + 9)/(x^2))` we want to divide by the highest denominator power.

`( (x)/(x^2) + (9)/(x^2))/ (x^2)/(x^2) \ \textgreater \ refine \ \textgreater \ (1)/(x) + (9)/(x^2)`
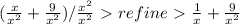
Write the exception again.

`\lim_(n \to \infty) (1)/(x) + \lim_(n \to \infty) (9)/(x^2)`
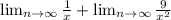
Apply the infinite property to both!
`\lim_(n \to \infty) ( (c)/(x^a) ) = 0 \ \textgreater \ \lim_(n \to \infty) (1)/(x) = 0 \ \textgreater \ \lim_(n \to \infty) (9)/(x^2) = 0 \ \textgreater \ 0 + 0 = 0`
For 3 apply
`\lim_(x \to a^c)= c \ \textgreater \ 3 \ \textgreater \ 0 + 3 = 3`
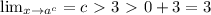
Now combine our terms and we get y = 2x + 3

Answer 2

It will look like this

There is no horizontal aseymtope, because it passes through all of possible y