Answer:
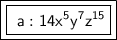
Solution Steps:
______________________________
1.) To solve this you must first know the formula for area of a rectangle:
- Area
 ×
×
- Area
 ×
×
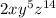
Note:
- It doesn't matter which measurement fills the height or width part in the formula.
Equation at the end of Step 1:
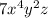 ×
×
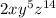
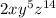 ×
×
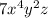
2.) Add 4 and 1, (x powers:)
Note:
- To multiply powers of the same base, you can add their exponents. So you just do
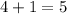 .
.
- When you have a plain variable like
 , you can assume
, you can assume
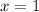 .
.
Equation at the end of Step 2:
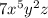 ×
×

3.) Add 2 and 5, (y powers:)
Note:
- To multiply powers of the same base, you can add their exponents. So you just do
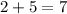 .
.
Equation at the end of Step 3:
 ×
×
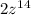
4.) Add 1 and 14, (z powers:)
Note:
- To multiply powers of the same base, you can add their exponents. So you just do
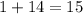 .
.
- When you have a plain variable like
 , you can assume
, you can assume
 .
.
Equation at the end of Step 4:
 ×
×
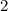
5.) Multiply 7 and 2:
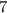 ×
×
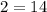
Note:
- Since we combine all the powers and multiplied the bases, all you have to do is put it all together in 1 form like we were doing after we added powers in the earlier steps.
Equation at the end of All Steps:
______________________________