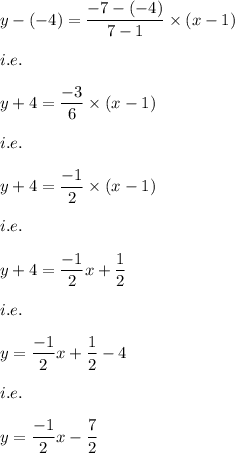Answer:
Yes, the relationship shown by the data linear.
The equation is given by:
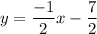
Explanation:
The table of values is given by:
x y
1 -4
7 -7
13 -10
19 -13
We know that the difference in each of the x-value is: 6
( Since, 7-1=6
13-7=6
19-13=6)
and if the difference in the each of the y-value is same then the relationship is linear.
( Since, a table of values represent a linear relationship if the rate of change is constant.
i.e. the ratio of change in y-values to the change in x-values)
Hence, we find the difference in y-value:
-7-(-4)= -3
-10-(-7)= -3
-13-(-10)= -3
Since, the difference in y-value is constant.
Hence, the relationship is linear.
Also, we know that the equation of the line will pass through (1,-4) and (7,-7)
Hence, the equation of line is calculated by: