Question

How does the graph of f(x) =-3^2x-4 differ from the graph of g(x)=-3^2x

Answer 1

`\bf ~~~~~~~~~~~~\textit{function transformations} \\\\\\ % templates f(x)={{ A}}({{ B}}x+{{ C}})+{{ D}} \\\\ ~~~~y={{ A}}({{ B}}x+{{ C}})+{{ D}} \\\\ f(x)={{ A}}\sqrt{{{ B}}x+{{ C}}}+{{ D}} \\\\ f(x)={{ A}}(\mathbb{R})^{{{ B}}x+{{ C}}}+{{ D}} \\\\ f(x)={{ A}} sin\left({{ B }}x+{{ C}} \right)+{{ D}} \\\\ --------------------`


`\bf \bullet \textit{ stretches or shrinks horizontally by } {{ A}}\cdot {{ B}}\\\\ \bullet \textit{ flips it upside-down if }{{ A}}\textit{ is negative}\\ ~~~~~~\textit{reflection over the x-axis} \\\\ \bullet \textit{ flips it sideways if }{{ B}}\textit{ is negative}\\ ~~~~~~\textit{reflection over the y-axis}`


`\bf \bullet \textit{ horizontal shift by }\frac{{{ C}}}{{{ B}}}\\ ~~~~~~if\ \frac{{{ C}}}{{{ B}}}\textit{ is negative, to the right}\\\\ \left. \qquad \right. if\ \frac{{{ C}}}{{{ B}}}\textit{ is positive, to the left}\\\\ \bullet \textit{ vertical shift by }{{ D}}\\ ~~~~~~if\ {{ D}}\textit{ is negative, downwards}\\\\ ~~~~~~if\ {{ D}}\textit{ is positive, upwards}\\\\ \bullet \textit{ period of }\frac{2\pi }{{{ B}}}`

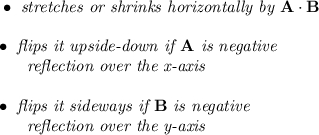
with that template in mind, let's check,


`\bf f(x)=-3^{\stackrel{B}{2}x\stackrel{C}{-4}}\qquad \qquad g(x)=-3^(2x)\implies g(x)=-3^{\stackrel{B}{2}x\stackrel{C}{+0}}`

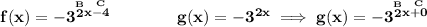
notice, g(x) has a horizontal shift of C/B or +0/2, or just 0, none.

while f(x) has a horizontal shift of C/B or -4/2, or -2, to the right.

so f(x) is really just g(x), but shifted horizontally over 2 units to the right.