Answer:
see explanation
Explanation:
There are 2 possible approaches to differentiating these.
Expand the factors and differentiate term by term, or
Use the product rule for differentiation.
I feel they are looking for use of product rule.
Given
y = f(x). g(x) , then
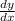 = f(x).g'(x) + g(x).f'(x) ← product rule
= f(x).g'(x) + g(x).f'(x) ← product rule
(a)
y = (2x - 1)(x + 4)²
f(x) = 2x - 1 ⇒ f'(x) = 2
g(x) = (x + 4)²
g'(x) = 2(x + 4) ×
 (x + 4) ← chain rule
(x + 4) ← chain rule
= 2(x + 4) × 1
= 2(x + 4)
Then
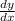 = (2x - 1). 2(x + 4) + (x + 4)². 2
= (2x - 1). 2(x + 4) + (x + 4)². 2
= 2(2x - 1)(x + 4) + 2(x + 4)² ← factor out 2(x + 4) from each term
= 2(x + 4) (2x - 1 + x + 4)
= 2(x + 4)(3x + 3) ← factor out 3
= 6(x + 4)(x + 1)
--------------------------------------------------------------------------
(b)
y = x(x² - 1)³
f(x) = x ⇒ f'(x) = 1
g(x) = (x² - 1)³
g'(x) = 3(x² - 1)² ×
 (x² - 1) ← chain rule
(x² - 1) ← chain rule
= 3(x² - 1)² × 2x
= 6x(x² - 1)²
Then
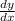 = x. 6x(x² - 1)² + (x² - 1)³. 1
= x. 6x(x² - 1)² + (x² - 1)³. 1
= 6x²(x² - 1)² + (x² - 1)³ ← factor out (x² - 1)²
= (x² - 1)² (6x² + x² - 1)
= (x² - 1)²(7x² - 1)
----------------------------------------------------------------------
(c)
y = (x² - 1)(x³ + 1)
f(x) = x² - 1 ⇒ f'(x) = 2x
g(x) = (x³ + 1) ⇒ g'(x) = 3x²
Then
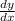 = (x² - 1). 3x² + (x³ + 1), 2x
= (x² - 1). 3x² + (x³ + 1), 2x
= 3x²(x² - 1) + 2x(x³ + 1) ← factor out x
= x[3x(x² - 1) + 2(x³ + 1) ]
= x(3x³ - 3x + 2x³ + 2)
= x(5x³ - 3x + 2) ← distribute
= 5
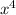 - 3x² + 2x
- 3x² + 2x
--------------------------------------------------------------------
(d)
y = 3x³(x² + 4)²
f(x) = 3x³ ⇒ f'(x) = 9x²
g(x) = (x² + 4)²
g'(x) = 2(x² + 4) ×
 (x² + 4) ← chain rule
(x² + 4) ← chain rule
= 2(x² + 4) × 2x
= 4x(x² + 4)
Then
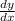 = 3x³. 4x(x² + 4) + (x² + 4)². 9x²
= 3x³. 4x(x² + 4) + (x² + 4)². 9x²
= 12
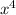 (x² + 4) + 9x²(x² + 4)² ← factor out 3x²(x² + 4)
(x² + 4) + 9x²(x² + 4)² ← factor out 3x²(x² + 4)
= 3x²(x² + 4) [ 4x² + 3(x² + 4) ]
= 3x²(x² + 4)(4x² + 3x² + 12)
= 3x²(x² + 4)(7x² + 12)