Question

What is the probability of making a type ii error when the machine is overfilling by .5 ounces (to 4 decimals)?

Answer 1

Part A

The probability of making a type ii error is equal to 1 minus the power of a hypothesis testing.

The power of a hypothesis test is given by:


`\beta(\mu')=\phi\left[z_(\alpha/2)+ (\mu-\mu')/(\sigma/√(n)) \right]-\phi\left[-z_(\alpha/2)+ (\mu-\mu')/(\sigma/√(n)) \right]`

Given that the machine is overfilling by .5 ounces, then
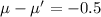
`\mu-\mu'=-0.5`, also, we are given that the sample size is 30 and the population standard deviation is = 0.8 and α = 0.05

Thus,


`\beta(16.5)=\phi\left[z_(0.025)+ (-0.5)/(0.8/√(30)) \right]-\phi\left[-z_(0.025)+ (-0.5)/(0.8/√(30)) \right] \\ \\ =\phi\left[1.96+ (-0.5)/(0.1461) \right]-\phi\left[-1.96+ (-0.5)/(0.1461) \right] \\ \\ =\phi(1.96-3.4233)-\phi(-1.96-3.4233) \\ \\ =\phi(-1.4633)-\phi(-5.3833)=0.07169`

Therefore, the probability of making a type II error when the machine is overfilling by .5 ounces is 1 - 0.07169 = 0.9283



Part B:

From part A, the power of the statistical test when the machine is overfilling by .5 ounces is 0.0717.