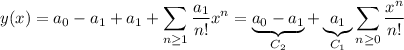Question

Find two power series solutions of the given differential equation about the ordinary point x = 0. compare the series solutions with the solutions of the differential equation obtained using the method of section 4.3. try to explain any differences between the two forms of the solution. y'' − y' = 0

Answer 1

I don't know what method is referred to in "section 4.3", but I'll suppose it's reduction of order and use that to find the exact solution. Take
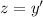
`z=y'`, so that
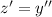
`z'=y''` and we're left with the ODE linear in
`z`:


`y''-y'=0\implies z'-z=0\implies z=C_1e^x\implies y=C_1e^x+C_2`

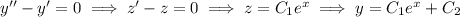
Now suppose
`y` has a power series expansion


`y=\displaystyle\sum_(n\ge0)a_nx^n`

`\implies y'=\displaystyle\sum_(n\ge1)na_nx^(n-1)`

`\implies y''=\displaystyle\sum_(n\ge2)n(n-1)a_nx^(n-2)`

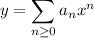
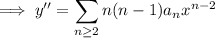
Then the ODE can be written as


`\displaystyle\sum_(n\ge2)n(n-1)a_nx^(n-2)-\sum_(n\ge1)na_nx^(n-1)=0`


`\displaystyle\sum_(n\ge2)n(n-1)a_nx^(n-2)-\sum_(n\ge2)(n-1)a_(n-1)x^(n-2)=0`


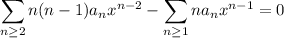
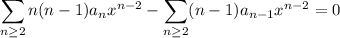
`\displaystyle\sum_(n\ge2)\bigg[n(n-1)a_n-(n-1)a_(n-1)\bigg]x^(n-2)=0`

All the coefficients of the series vanish, and setting
`x=0` in the power series forms for
`y` and
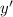
`y'` tell us that
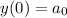
`y(0)=a_0` and
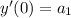
`y'(0)=a_1`, so we get the recurrence


`\begin{cases}a_0=a_0\\\\a_1=a_1\\\\a_n=\frac{a_(n-1)}n&\text{for }n\ge2\end{cases}`

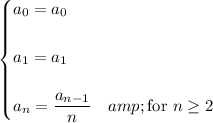
We can solve explicitly for
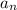
`a_n` quite easily:


`a_n=\frac{a_(n-1)}n\implies a_(n-1)=(a_(n-2))/(n-1)\implies a_n=(a_(n-2))/(n(n-1))`

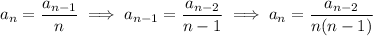
and so on. Continuing in this way we end up with


`a_n=(a_1)/(n!)`

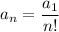
so that the solution to the ODE is


`y(x)=\displaystyle\sum_(n\ge0)(a_1)/(n!)x^n=a_1+a_1x+\frac{a_1}2x^2+\cdots=a_1e^x`

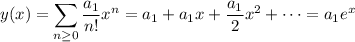
We also require the solution to satisfy
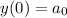
`y(0)=a_0`, which we can do easily by adding and subtracting a constant as needed:


`y(x)=a_0-a_1+a_1+\displaystyle\sum_(n\ge1)(a_1)/(n!)x^n=\underbrace{a_0-a_1}_(C_2)+\underbrace{a_1}_(C_1)\displaystyle\sum_(n\ge0)(x^n)/(n!)`