Answer: 0 and 1
=========================================================
Work Shown:
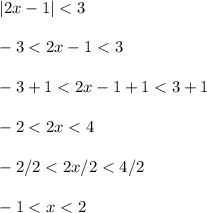
If x is a nonnegative integer, then writing -1 < x < 2 is the exact same as writing the roster notation {0, 1}. This is the solution set. We ignore anything negative and it must be a whole number smaller than 2.
------------
If we were to plug in x = 0, then we'd get a true statement

I'll let you try out x = 1. That should result in a true statement as well.
Trying out x = 2 or larger will result in a false statement.