Question

Point P is inside equilateral triangle ABC such that the altitudes from P to AB, BC, and CA have lengths 5, 6, and 7 respectively. What is the area of triangle ABC?

Answer 1

Looking at the first image attached (I don't have the best drawing skills by any definition of the word, sorry), I simply drew a line from P to AB, P to BC, and P to CA. Since it states 'altitudes', it means that we draw the lines to the middle of the sides. Seeing the second image attached, we have three triangles with base s (since it's equilateral, the s is the same) and the area of the triangles are as follows using the area of a triangle formula (base*height/2):
ABP=5s/2
BCP=6s/2
CAP=7s/2
Adding them all up, it's clear that they make up the area of the triangle. In addition, given that the area of an equilateral triangle with length s is

`(s^(2)* √(3) )/(4)` , we have

`(5s)/(2) + (6s)/(2) + (7s)/(2) = (s^(2)* √(3) )/(4) = (18s)/(2) =9s`

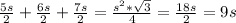
Multiplying both sides by 4, we have 36s=s²√3. Next, we can divide both sides by s to get 36=s√3 . After that, we can divide both sides by √3 to get
36/√3=s

Plugging that back into the equation
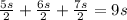
`(5s)/(2) + (6s)/(2) + (7s)/(2)=9s` for the area (we could have used the equilateral triangle formula,but that seemed a bit messy)., we get
(36/√3)*9=108*√3 as the area

Feel free to contact me with further questions!