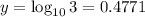Answer:
y=0.4771
Explanation:
Given : Using the graph of

To find : The value of y in the equation
 .
.
Solution :
Let,
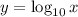
and

Now, we plot these two equations.
The graph of
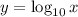 is shown with violet line.
is shown with violet line.
The graph of
 is shown with black line.
is shown with black line.
The solution to this system will be their intersection point.
The intersection point of these graph is (3,0.4771)
Refer the attached graph below.
Therefore, The value of y=0.4771
or we can verify it by,

Taking log both side,