Answer:
33,2 ≈ c
45 ≈ b
120° = A
Step-by-step explanation:
We will be using the Law of Sines:
Solving for Angle Measures
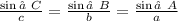
** In the end, use the sin⁻¹ function or else you will throw off your answer.
Solving for Sides
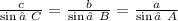
Given instructions:
Well, the first thing we can do is to find the m∠A, and we have to use the Triangular Interior Angles Theorem:
25° + 35° + m∠A = 180°
|________|
60° + m∠A = 180°
-60° - 60°
__________________
m∠A = 120°
Now that we have the third angle measure, we can use it in the formula to find the other sides of the triangle, like side c:
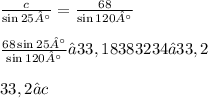
Now, we have to find side b:
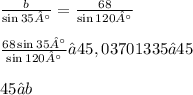
Now everything has been defined!
I am joyous to assist you anytime.