Question

Which of these four sets of side lengths will form a right triangle? Set 1 4 cm, 5 cm, 6 cm Set 2 8 in., 12 in., 20 in. Set 3 10 mm, 20 mm, 30 mm Set 4 12 ft, 16 ft, 20 ft Set 1 Set 2 Set 3 Set 4

Answer 1

D

Explanation:

because yes

Answer 2

Answer: The correct option is (D) SET 4.

Step-by-step explanation: We are to select the correct set of side lengths that will form a right-angled triangle.

To form a right-angled triangle, we must have the following relation:

Perpendicular² + Base² = Hypotenuse².

Hypotenuse is the length of the largest side; perpendicular and base are the two legs of the triangle.

SET 1 : 14 cm, 5 cm, 6 cm.

We have

`5^2+6^2=25+36=61,\\\\14^2=196.`

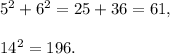
Therefore,

Perpendicular² + Base² ≠ Hypotenuse².

So, this set will not form a right-angled triangle.

SET 2 : 8 in., 12 in., 20 in.

We have

`8^2+12^2=64+144=208,\\\\20^2=400.`

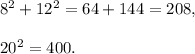
Therefore,

Perpendicular² + Base² ≠ Hypotenuse².

So, this set will not form a right-angled triangle.

SET 3 : 10 mm, 20 mm, 30 mm.

We have

`10^2+20^2=100+400=500,\\\\30^2=900.`

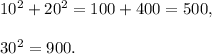
Therefore,

Perpendicular² + Base² ≠ Hypotenuse².

So, this set will not form a right-angled triangle.

SET 4 : 12 ft, 16 ft, 20 ft.

We have

`12^2+16^2=144+256=400,\\\\20^2=400.`

Therefore,

Perpendicular² + Base² = Hypotenuse².

So, this set will form a right-angled triangle.

Thus, the SET 4 will form a right-angles triangle.

Option (D) is correct.