Answer:
The correct option is C.
Explanation:
Given information: One side of the rectangle is (5x+2) and another sides of rectangle is (x-4).
The area of rectangle is
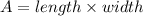
Substitute length = (5x+2) and width = (x-4) in the above formula, to find the simplified polynomial expression in standard form to represent the area of the rectangle.

Using distributive property,
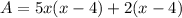
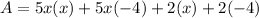
On simplification we get
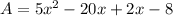
On combining like terms we get
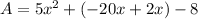
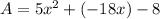
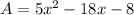
Therefore the correct option is C.