Answer:
Orbital period of the planet is 0.537 years.
Step-by-step explanation:
Given that,
A planet has an average distance to the sun of 0.66 AU,
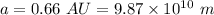
The orbital period of the planet is determined using Kepler's law of planetary motion. Mathematically, the Kepler's law is given by :
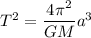
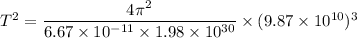
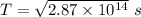
T = 16941074.34 s
or
T = 0.537 years
So, the orbital period of the planet is 0.537 years. Hence, this is the required solution.