Question

In this Triangle, cos a/cos b=___

Answer 1

Answer:
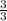`(3)/(3)` Or 1

Step-By-Step Explanation:

`\left[\begin{array}{ccc}Sine&(SinA)/(A)\\Rule&(SinB)/(B)\\&(SinC)/(C) \end{array}\right]`

`\left[\begin{array}{ccc}Cos&(CosA)/(A)\\Rule&(CosB)/(B)\\&(CosC)/(C) \end{array}\right]`

`\left[\begin{array}{ccc}(CosA)/(SinA)=(CosB)/(SinB)=(CosC)/(SinC) \end{array}\right]`

`\left[\begin{array}{ccc}CosA&=(3)/(4.24)\\CosB&=(3)/(4.24)\end{array}\right]`

Additional Answers:

Area: T = 4.5

Perimeter: p = 10.24

Semiperimeter: s = 5.12

Angle ∠ A = α = 89.929° = 89°55'43″ = 1.57 rad

Angle ∠ B = β = 45.036° = 45°2'8″ = 0.786 rad

Angle ∠ C = γ = 45.036° = 45°2'8″ = 0.786 rad

Height: ha = 2.123

Height: hb = 3

Height: hc = 3

Median: ma = 2.123

Median: mb = 3.352

Median: mc = 3.352

Inradius: r = 0.879

Circumradius: R = 2.12

Vertex coordinates: A[3; 0] B[0; 0] C[2.996; 3]

Centroid: CG[1.999; 1]

Coordinates of the circumscribed circle: U[1.5; 1.498]

Coordinates of the inscribed circle: I[2.12; 0.879]

Exterior(or external, outer) angles of the triangle:

∠ A' = α' = 90.071° = 90°4'17″ = 1.57 rad

∠ B' = β' = 134.964° = 134°57'52″ = 0.786 rad

∠ C' = γ' = 134.964° = 134°57'52″ = 0.786 rad

Answer 2

cos A = 3/4.24 and cos B = 3/4.24 also.

The ratio of cos A to cos B is thus 3/3, or 1 (answer)