Question

Let us denote by P the set of all people, by S the set of people who are single, by C the set of people who have children, by W the set of women and by M the set of men. For each question below, write down an expression that represents the set being described. Write exactly one expression for each question.

a. Women who are either married with children, or single and do not have children.
b. All possible married heterosexual couples, i.e., all possible pairings of married men and married women.
c. The number of all possible married heterosexual couples.

Answer 1

Given :

The events are as follows :

P : Set of all the people

S : Set of people those who are single

C : Set of people having children

W : Set of women

M : Set of men

a). Now set of married women having children is given by :

`$\left( (P-S)-M \right) \cap C $`

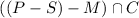
And set of single women who do not have any children : (S -C) - M

Thus the set of women those who are either married and have children or they are single and they do not have any children is represented by :

`$\left( (S-C)-M\right) \cup \left( ((P-S)-M) \cap C \right) $`

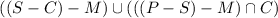
b). Set of Married men :
`$\left( (P-S) \cap M$`

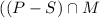
Set of Married men :
`$\left( (P-S) \cap W$`

Set of all possible married who are heterosexual couples, that is, all possible pairings of the married men and the married women is represented by :

`$((P-S) \cap M) \cap ((P-S) \cap W )$`

c). The number of all the possible married heterosexual couples will be represented by the cardinality of the above set, which represents the number of the elements in the set.

Thus the number of the married heterosexual couples is given by :

`$n[((P-S) \cap M) \cap ((P-S) \cap W)]$`