Answer:
The calculated value t = 3.5648> 1.9842 at 0.1 level of significance
The null hypothesis is rejected
The mean of the sample does not come from the Population
Explanation:
Step(i):-
Given that sample size 'n' = 100
Mean of the sample x⁻ = 315.40
The standard deviation of the sample (s) = 43.20
Level of significance = 0.1
Mean of the Population = 300
Null hypothesis: H₀: x₀ = μ
Alternative Hypothesis: H₁: x₀ ≠ μ
Step(ii):-
Test statistic
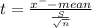
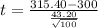
t = 3.5648
Degrees of freedom = n-1 = 100-1 =99
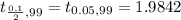
The calculated value t = 3.5648> 1.9842 at 0.1 level of significance
The null hypothesis is rejected
The mean of the sample does not come from the Population