Question

How to determine if the columns of a matrix are linearly independent?

Answer 1

Let's consider an arbitrary 2x2 matrix as an example,


`\mathbf A=\begin{bmatrix}\mathbf x&\mathbf y\end{bmatrix}=\begin{bmatrix}x_1&y_1\\x_2&y_2\end{bmatrix}`

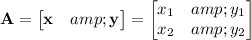
The columns of
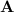
`\mathbf A` are linearly independent if and only if the column vectors
`\mathbf x,\mathbf y` are linearly independent.

This is the case if the only way we can make a linear combination of
`\mathbf x,\mathbf y` reduce to the zero vector is to multiply the vectors by 0; that is,


`c_1\mathbf x+c_2\mathbf y=\mathbf 0`

only by letting
`c_1=c_2=0`.

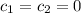
A more concrete example: suppose


`\mathbf A=\begin{bmatrix}1&2\\4&8\end{bmatrix}`

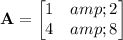
Here,
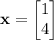
`\mathbf x=\begin{bmatrix}1\\4\end{bmatrix}` and
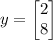
`\amthbf y=\begin{bmatrix}2\\8\end{bmatrix}`. Notice that we can get the zero vector by taking
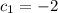
`c_1=-2` and
`c_2=1`:


`-2\begin{bmatrix}1\\4\end{bmatrix}+\begin{bmatrix}2\\8\end{bmatrix}=\begin{bmatrix}-2+2\\-8+8\end{bmatrix}=\mathbf 0`

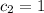
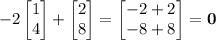
so the columns of
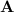
`\mathbf A` are not linearly independent, or linearly dependent.