Answer:
A. The graph of f(x) = |x| is shifted to the left 8 units, down 3 units.
Explanation:
We are given,
The transformed function is
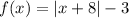 .
.
Now, the parent function is
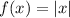 .
.
So, we have,
When the parent function is shifted 8 units to the left, the function is
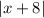 .
.
This function when translated 3 units downwards gives
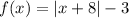 .
.
Thus, we get,
The parent function f(x)=|x| is translated 8 units to the left and 3 units downwards.
So, option A is correct.