Answer:
Therefore,
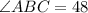
Explanation:
We need to find the
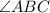
Since,
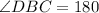 ( since DBC is straight line )
( since DBC is straight line )
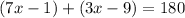
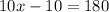
Add both the sides by 10 in above expression
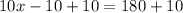
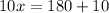
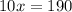
divide both the sides by 10 in above expression
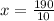

Hence, the value of x is 19.
Now, we will calculate
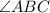
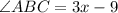
Put x = 19 in above
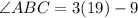
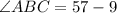
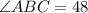
Therefore,
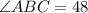 .
.